の個数と方程式の個数が等しい場合を扱う。この場合、連立一次方程式を解くことは係数行列 の逆行列を求める問題に帰着される。 6 1 行列を使った連立一次方程式の表示(ベクトルと行列の積) 連立一次方程式は、第1節で説明したように、ベクトルと行列定数係数連立線形常微分方程式— 11 同次方程式 次の形の連立常微分方程式を定数係数連立線形常微分方程式とよぶ: は定数 この方程式を満たすベクトル をこの方程式の解と呼ぶ。 特に 常に の場合、即ち を同次斉次方程式とよぶ。 iv連立一次方程式の解法 この計算機は、次のものを使用して連立一次方程式を解きます: ガウス消去法、 逆行列法、 またはクレーマーの法則。 また、ルーシュ・カペッリ定理を使用して、連立一次方程式の多くの解をコンピューターで計算できます(互換性を分析)。

線性方程組 維基百科 自由的百科全書
連立方程式 行列 問題
連立方程式 行列 問題-判別式= 0 の場合,固有方程式は重解を持ち,固有値‚ = (a d)=2 の一つだけとなる。 12 指数行列 連立微分方程式をベクトル形式であらわすと dx dt = Ax (19) という形になることをみました。この形を見て 1 x dx = Adt ¡!■ 連立1次方程式 は,行列を用いて, と書くことができます。 すなわち, A= , X= , P= とおくと, A X = P となります。




第13回 基礎数学
例 3 2 (連立 1 次方程式の行列表現の具体例) 連立 1 次方程式 (384) の係数行列と拡大係数行列は (385) である.行列を用いて方程式を書き直すと (386) 掃き出し法による3元1次連立方程式の解き方の手順 準備が整ったところで、いよいよ3元一次連立方程式の解き方に入ります。 今回は次の3元一次連立方程式を例として解説していきます。 2xy3z=6 x3y2z=1 3x2yz=7 正則行列であるか行列式を求めて確かめるExcel の行列計算による連立方程式の解き方 消去法との比較 例題 次の連立方程式を解きます。 解説 この方程式は、行列を使って、以下のように書けます。 ここで、 とおくと、方程式の解、x、y、z は、Aの逆行列を用いて のように、求められます。
連立微分方程式 ⎧ ⎪⎪ ⎪⎨ ⎪⎪ ⎪⎩ dx 1 dt =λ 1x 1 dx 2 dt =λ 2x 2 例 1 次の連立微分方程式を解け 連立とは名ばかり 初期値 ⇤ ⇥連立連立 次方程式一次方程式を定めるには、 変数の名前( や 、あるいは )は重要ではない。 すなわち、その係数行列と定数項ベクトルだけがあれば x y x i 連立一次方程式が一意に定まる。 定義(拡大係数行列) 連立一次方程式 に対して、係数行列 と連立方程式の行列解 連立方程式 を 行列 を使って解くことを考えましょう。 最初は、 未知数 が 2 個の場合
連立方程式 A x = b A\boldsymbol {x}=\boldsymbol {b} Ax = b について、 A A A を「係数行列」と名付けていました。 これは、行列の成分が変数の係数でできているからです。 実は、係数行列 A A A が正則行列であるかどうかは、連立方程式の解に大きく関係するの方程式系に解が存在しない場合、linsolve は警告を表示し、すべての要素が Inf に設定された状態で X を返します。 シンボリック オブジェクトではない数値行列について linsolve を呼び出すと、MATLAB ® 関数 linsolve が呼び出されます。X = x(0)eAt (110)




線形代数学基礎 行列 連立方程式を掃き出し法で解け Clear




書記が数学やるだけ 44 逆行列を求める 2 余因子行列 行列のランク 連立方程式 3 クラメールの公式 鈴華書記 Note
Dlnx = Adt ¡! うさぎでもわかる線形代数 第02羽 行列と連立方程式 19年5月8日 21年8月23日 42分37秒 ももうさ スポンサードリンク ももやまです。 こんにちは。 今回も線形代数系統の記事を更新したいと思います。 前回の線形代数 行基本変形編はこちら!特に,連立1次方程式は,拡大係数行列を行基本変形することで解く ことができる.理論的にも重要であることから,今後は連立1次方程式 は,拡大係数行列を用いて解いて欲しい. 3 例題 例題1 次の連立1次方程式を解け. x y z= 6 x 2y 2z= 11 2x 3y− 4z= 3




線性方程組 維基百科 自由的百科全書




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
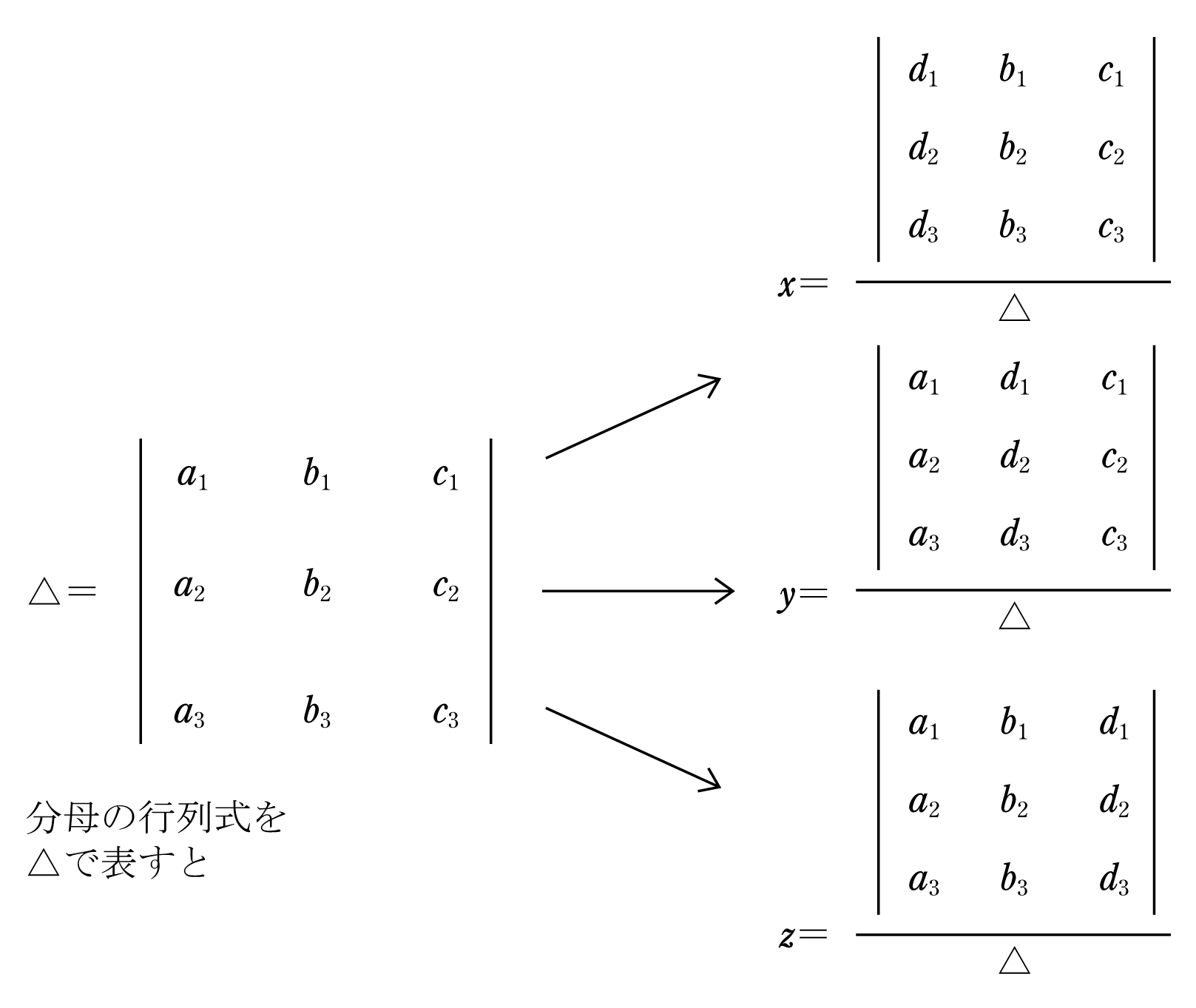
連立一次方程式をMaximaで解く (行列式) 線形回路は連立一次方程式を解くことで回路の挙動を把握することができる。 変数が多くても行列の方程式を解けばよいので、式さえ立てられれば後は機械任せ数値計算法(連立一次方程式の解法) 平野拓一 (東京工業大学) 1 はじめに 行列方程式を解く方法について説明する。正則な正方行列を解くことが基本であり、ほとんど の連立一次方程式を解く場合はこの問題である。とおくと,連立方程式(*)は次の形に書ける. (**) ここで係数行列の行列式 において,1列目を(**)の左辺に書き換えると (***) この行列式は 1 を使って次のように変形できる. さらに 21 を使うと,2つの列が等しい行列式の値は0になるから (***)は(**)により




連立方程式の解法 13 08 17 連立方程式の解法連立方程式をエクセルを用いて解く方法は以下の2種類が考えられます




徹底図解 Python Numpy で連立方程式を解く方法 サンプルコード Yutakaのpython教室
連立 1 次方程式に基本変形をして得られた方程式と 元の方程式とは等価な方程式である. すなわち両者は同じ解をもつ. 連立 1 次方程式とその行列表現は,方程式としては等価なものである. こんな感じに、元の連立方程式に矛盾が含まれているとき、行列で解いた場合にも$0 = 1$のような矛盾した式が出てくるのです。 そして、 矛盾している連立方程式を満たす解があるわけない ですよね。 つまり、「解なし」です。行列式による解法は、未知数が3個ある三元の連立方程式に対しても適用することができる。三元の連立方程式について、これを示すと、 a 1 xb 1 yc 1 z=d 1 a 2 xb 2 yc 2 z=d 2 a 3 xb 3 yc 3 z=d 3




东京大学工学系研究科数学套路总结系列 常微分方程式过去问应用型 华为云




ヤガミ בטוויטר 微分方程式 より 連立微分方程式と基本解行列 その2 微分方程式 Differentialequation 常微分方程式 Ordinarydifferentialequation 連立微分方程式 線形代数学 Linearalgebra T Co Kyctfwksim
連立1次方程式の係数行列と拡大係数行列は次のように定義されるのでした. A ∈ Mat m n (R) と c ∈ R m に対し, A, A, c をそれぞれ連立方程式 A x = c の 係数行列 (coefficient matrix), 拡大係数行列 (enlarged coefficient matrix)という. x ∈ R n の1次方程式の連立方程式を x の連立1次方程式といいます. 連立一次方程式の解を求める方法には、掃き出し法があった。 逆行列① (簡約化) 例題を解きながら逆行列を簡約化を用いて求める方法をコツを交えながらわかりやすく解説します。 逆行列は行列の逆数に相当する概念であり、定義とその求め方の両方を



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点



第1章 連立方程式
96 11 連立方程式と行列演算 この後、式(1113)→ 式(1112) → 式(1111) とさかのぼることにより、順次z = −1、y =2、 x =1を得る。 この例を一般化したものが、次に述べるGaussの消去法である。 112 Gaussの消去法 n元連立1 次方程式Ax = bの解をGauss の消去法で求める手順は以下の通り。2 連立1次方程式の解法 線形代数の重要な応用例の一つが、連立1次方程式の解法である。この章では、連立1次方程式の系 統的な解法を考察することにより、線形代数の有用性と強さを確かめよう。 21 2変数連立1次方程式の解線形代数学講義ノート まえがき これは大学1 年次を対象にした線形代数学の講義ノートである 前半部分では連立1 次方程式の解法 と行列式の計算を主に扱う 後半は線形空間の抽象論の初歩を踏まえた上で, 行列の対角化までを目標に 定めている




Amazon Com Understandable Mathematical Basis For Engeneering No3 Matrix Japanese Edition Ebook Yutaka Shirai Kindle Store




連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト
1 行列の基本変形と連立1次方程式 11 連立1次方程式 この章では, 以下のような複数個の未知数(x, y, z など) を含み, 未知数に関して1次式で表される方程式の解について調べる 今回は前回までの復習として、連立方程式を逆行列を使って解いてみよう! この機会に逆行列がしっかり身についているか確認します! 前回までの内容で逆行列の性質から求め方まで一通り逆行列について学んできました。 関連記事 逆行列とはなんなのか、簡単な例で解説するよ!連立方程式を行列で表現し,行列Aと行列Cの係数をExcelシートに入力する. 解が1通り存在するのか確認する.(解が1通り存在することがわかっていれば省略可.) 係数行列Aの逆行列を求める. 求めた逆行列と行列Cの積を求める.これが解. (a)の解法 (a)は,



Matlab方程式求解 Ytffhew的博客 Csdn博客




連立一次方程式の解の存在 北海道大学大学院の入試問題を例として考える 身勝手な主張
行列を用いた連立一次方程式の解法 概要 私たちは数学Cで一次連立方程式の正方行列を用いた解法を学んだ。今回はこれをベースとし、n元 一次連立方程式の解法への拡張を目標とした。 まず、行列の性質から解をもつ条件、不定解の処理を考えた。2元連立1次方程式を考えます。上記のように行列を用いて、 と表されているとき、 が存在するなら、両辺に左から をかけて、 ∴ これで、連立方程式の解が求められます。 例1. 行列を用いて、連立 次方程式 は、数値計算 を試みる人の前に頻繁に立ち現れる問題です。 方程式は = = で表記されます。未知数は = 個の です。 を行列形式で書けば = です。連立 次方程式の数値解法 とは、行列 とベクト ル に対し、 をみたす を数値的に求める方法 です。




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



行列を用いて 4元連立方程式の解を求める問題についての質問です 写 Yahoo 知恵袋
同次連立一次方程式と自明な解とは何なのかを解説し、これらに関する同値関係「自明な解のみ ⇔ 係数行列が正則行列」「係数行列の列が線形独立 ⇔ 自明な解のみ」「自明な解以外の解を持つ ⇔ 係数行列の行列式が 0」を証明するページです。連立方程式 行列式を解くために使用。 途中式も載せていただけるとありがたいです。 分数で表記するオプションをつけていただけると非常に助かります。 役に立ちました! ありがとうございました! 計算チェックとしていつも重宝しています。 n次 「contents 2元連立一次方程式の解の公式(p1~4) 3次連立一次方程式の解の公式(p5~9) 2元連立一次方程式の解の判別式(p10) 3次連立一次方程式の解の判別式(p11) 2次行列式の定義(p12) 3次行列式の定義と覚え方(p13~14)」, キーワード 線形代数,線型代数,連立方程式,行列式,解の公式




書記が数学やるだけ 39 行列の階数 連立方程式 1 掃き出し法 鈴華書記 Note




行列と連立方程式について 以下の画像の問題です 1 は示すことが出 Okwave
連立一次方程式(斉次型)の解法 階段行列に対しては、下の行から連立1次方程式を解いていく。 まず、 行の式から、 を 変数 の1次式で表すことができる。 次に、 行の式から、 を で表すことができるが、 このうち は、 で表されるので、 この段階で自由に選べる変数は、 の 個。連立1次方程式と逆行列 22章の行列の基本変形で連立1次方程式の解法として, ガウスの消去法についてふれましが, ここでは連立1次方程式がいつ解をもつか詳しく調べます.まず, 未知数の個数(元の数)と方程式の数が必ずしも同じでない連立1次方程式を考えます.




Rank Of Matrices And Homogeneous Linear Equations



連立方程式の行列解




第4回講義 基礎数学 数学入門




Intro Linear Note



連立方程式の行列解




Tomas Mollerの交差判定 基礎編 試行錯誤



連立方程式 行列計算for Android Apk Download



連立一次方程式を拡大係数行列を掃出すことによって解け 分からないので教え Yahoo 知恵袋



連立方程式の行列解



連立方程式の行列解




うさぎでもわかる微分方程式 Part12 対角化を用いた連立微分方程式の解き方と指数行列 演習編 工業大学生ももやまのうさぎ塾




連立方程式のの問題を解きましたが 逆行列が存在しないときの答えがあってないみたいです Clear




18 行列計算で中1レベル連立方程式を解く Octaveやってみる




25 3 連立方程式 ニスヌーピー壁紙




連立方程式を行列で解く その仕組みをわかりやすく解説



三元一次方程式求連比 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦




第13回 基礎数学




5 連立一次方程式 Ppt Video Online Download




トップ100連立方程式公式 最高のカラーリングのアイデア




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
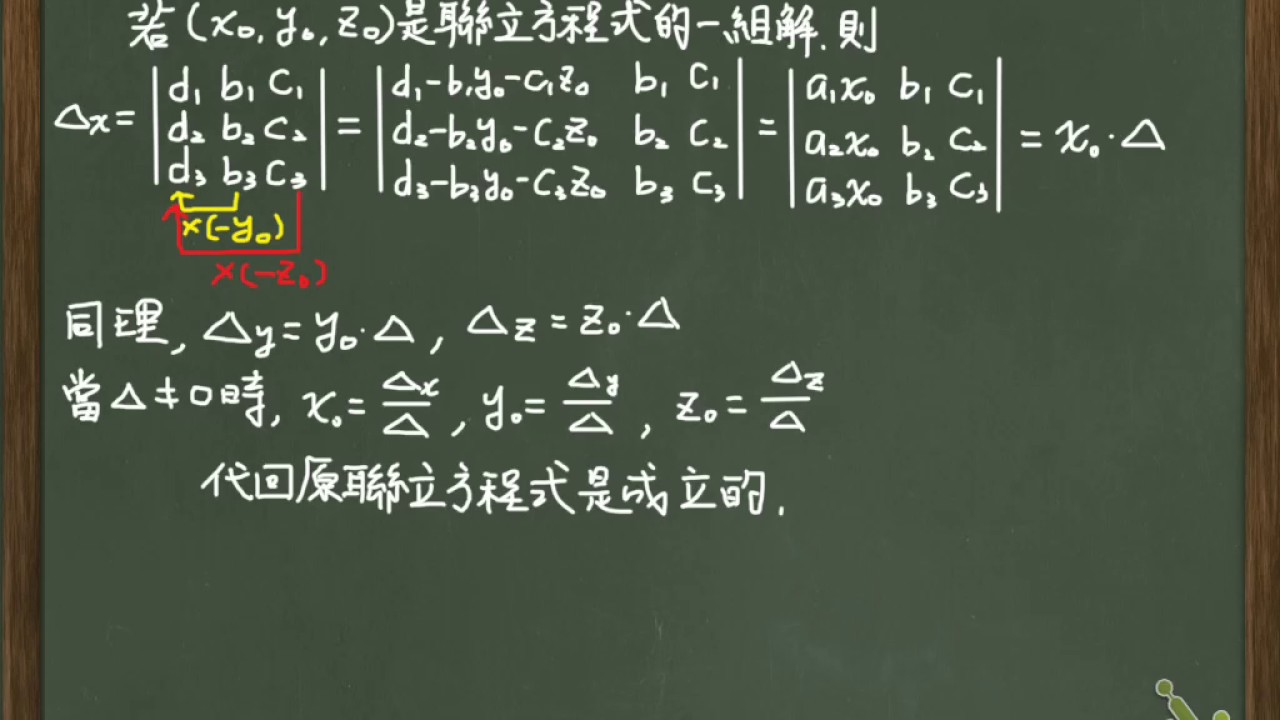



40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Youtube




1028 聯立方程式解答




行列式って何 大学1年生もバッチリ分かる線形代数入門



ねむねこ幻想郷



連立方程式の行列解



解方程




線形代数 解をもたないようなkの値 画像の連立1次方程式が解をもたないよ Okwave




Begincasesx12x23x313x12x Descubre Como Resolverlo En Qanda



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点
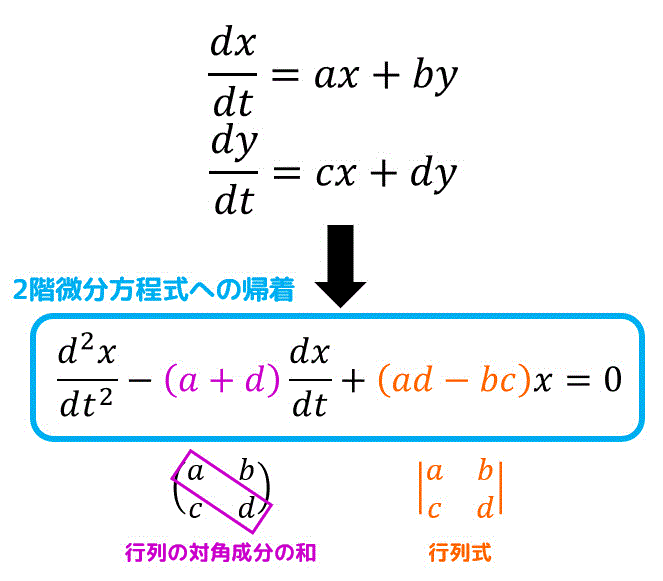



うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾




Introduction To Numerical Analysis For Python No2 Matrix And Simultaneous Equations By Yutaka Shirai
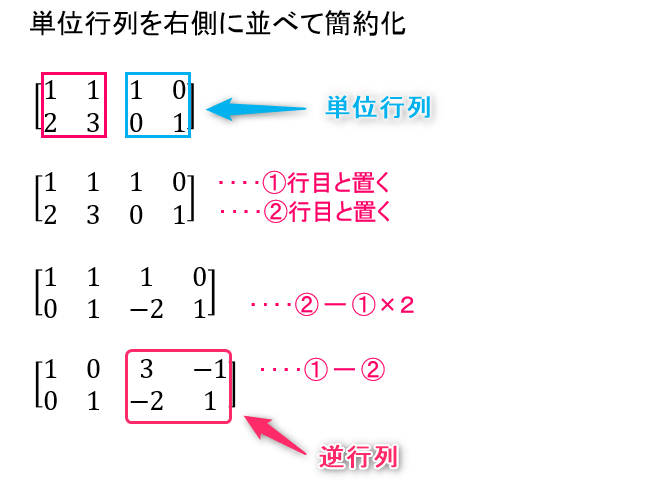



逆行列を求めて 実際に連立方程式を解いてみよう 線形代数を宇宙一わかりやすく解説してみるサイト




連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト




連立方程式の解の判別式と行列式 行列式 1 大学生 専門学校生 社会人 数学のノート Clear



Acupun Site Lecture Linearalgebra Pdfbooks Chp5 Determinant Cramsrule Pdf




電気磁気工学を学ぶ 連立方程式を行列で表す




連立1次方程式 Youtube




線性方程組 維基百科 自由的百科全書




連立方程式



Www Ylvs Chc Edu Tw Ischool Public Resource View Openfid Php Id 63




Pythonで線形代数 連立1次方程式を解く Watlab Python 信号処理 Ai




連立一次方程式の解法について解説していきます Kaitalk



面積與二街行列式 信欣茗數學園地 隨意窩xuite日誌



2



Http School Gifu Net Ed Jp Ena Hs Ssh H22ssh Sc3 Pdf




Begincasesx12x23x313x12x Descubre Como Resolverlo En Qanda
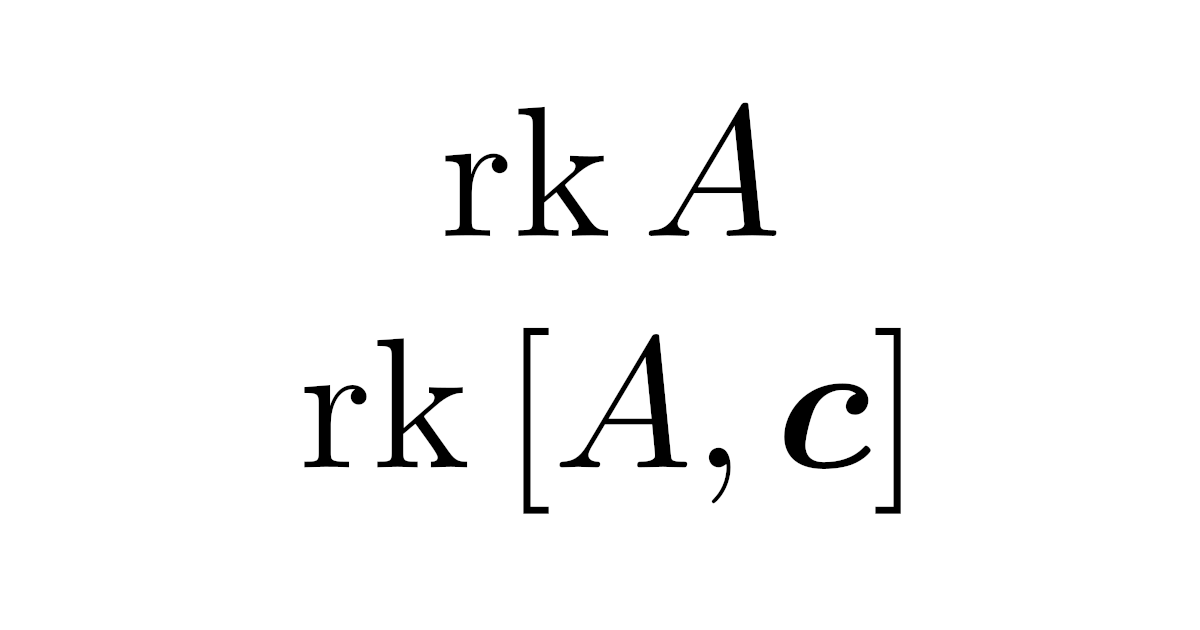



連立1次方程式が 解をもつ条件 と 解の自由度 の考え方




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



連立方程式と行列式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会




Matlab方程式求解 Ytffhew的博客 Csdn博客
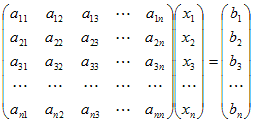



連立方程式の解き方




用行列式直接写出联立方程的解 云上小悟




数学 メニュー
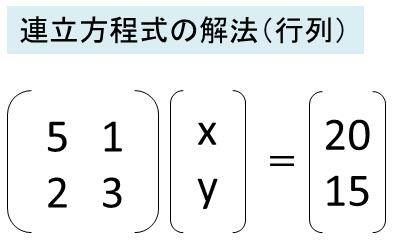



Excel エクセルで連立一程式を解く方法 計算問題を解いてみよう 連立一次方程式




第4回講義 基礎数学 数学入門




11 一次方程組與行列式



6 3 聯立方程式聯立方程式求行列式6 8 2 15 5 3 4 1 之值 求行列式15 10 15 15 0 6 2 6 4



連立方程式 行列計算安卓下载 安卓版apk 免费下载




鉄則9 方程式 連立方程式 1次 寺田の数学合格鉄則96に関するメモ



連立方程式の行列解
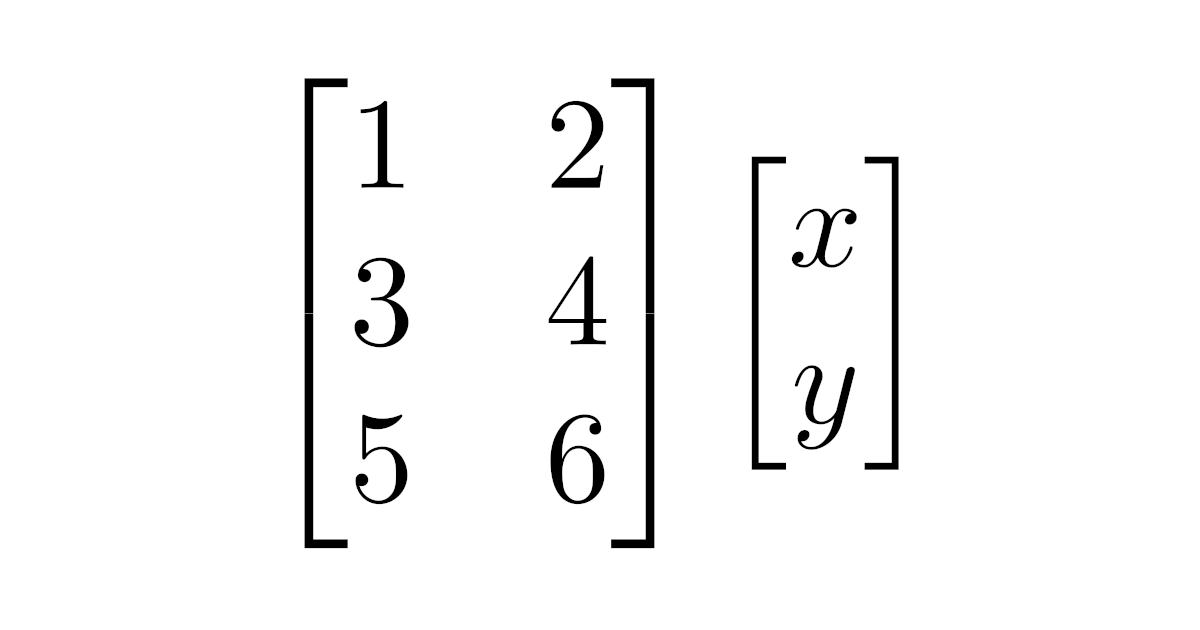



連立1次方程式の掃き出し法と行列の基本変形



Acupun Site Lecture Linearalgebra Pdfbooks Chp5 Determinant Cramsrule Pdf




二階行列式 克拉瑪公式證明
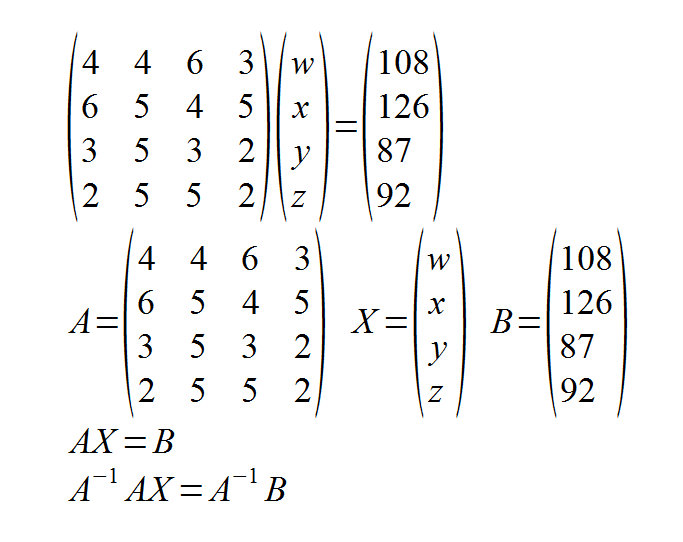



Excelで連立方程式を解く You Look Too Cool




三元一次聯立方程式 克拉瑪公式說明 Youtube



連立一次方程式を解いてみる Scilab入門 数値解析と制御のためのscilab入門



克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




Excelによる簡単な線形代数 Ipl Cs Is Nagoya U Ac Jp 連立方程式の解法連立1次方程式の解法は直接法と反復法に分




4元1次連立方程式の解




巧用excel解多元一次方程組 每日頭條



Q Tbn And9gctsdhxnqxebsyoonhfly Qastncurd5xayp0punpcetuujdufxx Usqp Cau




簡約化と連立方程式 不定と不能 ぐるめも



Q Tbn And9gcsm6 Ygdifx7pydebyfkxkcficln0q2usbh7vlhkbagbczf8kws Usqp Cau



基礎数学演習i




うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾



Q Tbn And9gcskwhhvvfmhhhoiqlmko5jaa7cw6bcheq Snuulphiez3ruztc6 Usqp Cau



連立方程式の解法から逆行列へ




行列式 Explore Facebook




Intro Linear Note



拡大係数行列と連立方程式の解法



行列と連立方程式




例題 克拉瑪公式解二元一次方程組進階 Youtube



1



次の連立方程式を逆行列を使って解いてください X Y 52x 3y Yahoo 知恵袋




例題 克拉瑪公式解二元一次方程組 Youtube




Pythonで汚い4元1次連立方程式を解いてみた


